|
TigerJython | xx für Gymnasien |
Forum
Zufallszahlen verwenden
# Tu8.py from gturtle import * import random def star(x, y): setPos(x, y) fillToPoint(x, y) for i in range(6): forward(10) right(140) forward(10) left(80) makeTurtle() hideTurtle() clear("blue") setPenColor("yellow") for i in range(50): x = random.randint (-270, 270) y = random.randint (-270, 270) star(x, y) |
|
Programmcode markieren
|
Erklärungen zum Programmcode:
| Mit clear("blue") wird der Hintergrund gelöscht und mit der blauen Farbe gefärbt | |
| import random importiert das Modul random | |
| x = random.randint(-270, 270) liefert eine Zufallszahl zwischen -270 und 270. Da die Funktion zum Modul random gehört, muss random. vorangestellt werden | |
| fillToPoint(x, y) füllt die Stern-Figur vom Punkt in welchen die Turtle mit dem Zeichnen des Sternes beginnt |
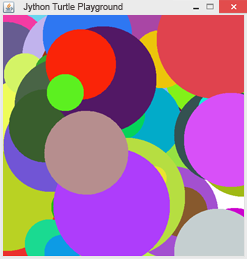
Beispiel 2: Zufälliges malen Eine zufällige Farbe wird erzeugt, indem man für den Rot-, Grün- und Blau-Anteil des RGB-Werts eine ganzzahlige Zufallszahl zwischen 0 und 255 wählt.
|
 |
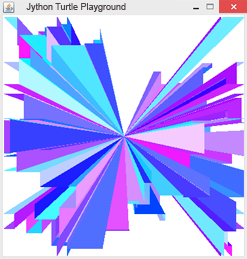
Beispiel 3: Noch ein Kunstwerk Die Turtle bewegt sich um eine zufällig gewählte Strecke vorwärts und dreht zufällig um 90° nach links oder rechts. Der blaue Farbanteil wird hier auf 255 gesetzt.
|
 |
Erklärungen zum Programmcode:
| Mit wrap() wird Turtle in den wrap-Modus versetzt. Wenn sie am Rand des Fensters ankommt, erscheint sie automatisch auf den gegenüber liegenden Rand des Fensters (Torussymmetrie) |
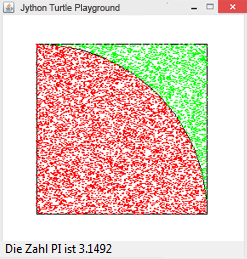
Beispiel 4: Berechnung von π mit Zufallsregen
Die Überprüfung, ob ein Zufallspunkt im Viertelkreis liegt, erfolgt nach dem Satt von Pythagoras. Summe der Quadrate der beiden Koordinaten muss kleiner als 1 sein.
|
 |
Erklärungen zum Programmcode:
| Für die Berechnung werden mit random.random() Zufallszahlen zwischen 0 und 1 erzeugt. Für die grafische Darstellung werden diese Zahlen mit 200 multipliziert. Auch die Quadratseite ist hier nicht 1 sondern 200. |
Beispiel 5: Beliebige Fläche mit Monte-Carlo-Methode berechnen In unserem Beispiel soll die graue Fläche berechnet werden. Die Überprüfung, ob ein Zufallspunkt in dieser Fläche liegt, kann durch Erfassung der Hintergrundfarbe vorgenommen werden. Mit getPixelColorStr(), kann man die Pixelfarbe an der aktuellen Turtleposition bestimmen. Wenn diese "gray" ist, so liegt der Punkt in der grauen Fläche und wird als Treffer erfasst. |
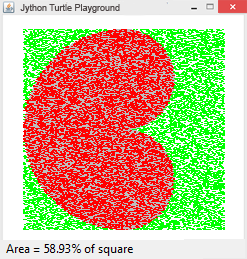 |
# Tu8d.py from gturtle import * import random def figure(): setPenColor("gray") setFillColor("gray") setPos(0, 100) startPath() rightArc(100, 90) rightArc(50, 180) left(180) rightArc(50, 180) rightArc(100, 90) fillPath() makeTurtle() hideTurtle() figure() n = 20000 hits = 0 addStatusBar(20) for i in range(n): zx = random.randint(0, 200) zy = random.randint(0, 200) setPos(zx, zy) if getPixelColorStr() == "gray" or getPixelColorStr() == "red": hits = hits + 1 setPenColor("red") else: setPenColor("green") dot(2) a = hits/n * 100 setStatusText(" Area = " + str(a) + "% of square") |
| Programmcode markieren
|
Erklärungen zum Programmcode:
| Da nur Pixel mit ganzzahligen Koordinaten für die Farbüberürüfung genommen werden, werden hier ganzzahlige Zufallszahlen verwendet. Der theoretisch berechnete Wert der grauen Fläche beträgt 58.9% der Quadratfläche. | |
| getPixelColorStr() == "gray" or getPixelColorStr() == "red": Die Punkte können mehrmals getroffen werden. Die bereits rot-gefärbte Punkte müssen daher auch als Treffer gezählt werden. |
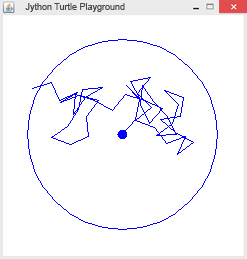
# Tu8e.py from gturtle import * import random makeTurtle() hideTurtle() addStatusBar(20) dot(10) openDot(400) n = 0 r = 0 while r < 200: z = random.random() angle = z * 360 heading(angle) forward(20) r = distance(0, 0) setStatusText("Number of steps: " + str(n) + ". Distance: " + str(r)) n += 1 |
| Programmcode markieren
|
Erklärungen zum Programmcode:
| heading(angle): Legt die Richtung der Turtle fest | |
| distance(0, 0): Gibt die Distanz der zwischen der aktuellen Turtle-Position und dem Punkt(0, 0) zurück |
| Aufgaben Serie 8 |
1) |
Zeichne Konfetti in den Farben rot, magenta, yellow, cyan und green an zufällig gewählten Positionen. Wähle einen schwarzen Hintergrund. |
 |
|||
2) |
Zeichne gefüllte Rechtecke mit zufällig gewählten Breite und Höhe, an zufälligen Positionen und mit zufällig gewählten Farben.
|
 |
|||
3) |
Bestimme mit dem Zufallsregen die Fläche der nebenstehenden Figur. Verwende das unten stehende Programm, um die Figur mit grauer Farbe zu erzeugen und lasse die Zufallspunkte auf ein Quadrat mit der Seitenlänge 300, in welches diese Fläche eingebettet ist, fallen.
|
 |
|||
4) |
Schreibe ein Programm, welches das zufällige Wandern einer Turtle (siehe Beispiel 6) 100 mal wiederholt. Wie viele Schritte braucht die Turtle im Durchschnitt, um den Rand des Geheges, der die Entfernung 200 von ihrem Startpunkt hat, zu erreichen?
|
 |
|||
5) |
Die Anfangs- und Endpunkte der Strecken werden mit Zufallszahlen zwischen -300 und 300 bestimmt. Die gefüllten Kreise liegen jeweils in der Mitte (xm = (x1 + x2) / 2, ym = (y1 + y2) / 2). |
 |