# Gp12a.py from gpanel import * makeGPanel(-6, 6, -30, 30) drawGrid(-5, 5, -25, 25, "gray") setColor("blue") lineWidth(2) x = -5 while x < 5: y = x ** 3 - 9 * x pos(x, y) if x == -5 else draw(x, y) x = x + 0.01
Für die Darstellung der Funktionsgrafen stehen im Modul gpanel einige praktische Werkzeuge zur Verfügung. Das Koordinatensystem kann beim Erzeugen des Grafikfensters mit makeGPanel() frei gewählt werden. Ein Koordinatengitter wird mit der Funktion drawGrid() erstellt. Dabei wird der x- und y-Bereich sowie die Gitterfarbe festgelegt.
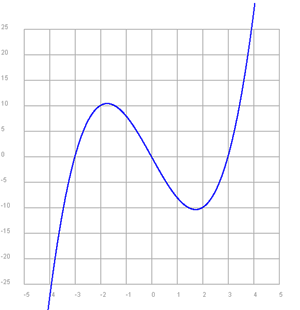
Beispiel 1: Eine Funktion darstellen und das Koordinatengitter verwenden
Im Beispiel wird die Funktion y =x3 - 9x im Koordinatensystem dargestellt. Mit drawGrid(-5, 5, -25, 25, "gray") wird das Koordinatengitter im x-Bereich -5..5 und im y-Berich -25..25 in grauer Farbe gezeichnet. Das GPanel-Fenster muss etwas grösser gewählt werden, damit die Beschriftung der Achsen Platz hat. Meist vergrössert man den Bereich auf allen Seiten um 10%, also hier x im Bereich -6..6 und y im Bereich -30..30.
In eine while-Schleife wird im Bereich -5 bis 5 in kleinen Schritten der Funktionswert berechnet un mit der Funktion draw(x, y) dargestellt. Dabei wird der neue Punkt automatisch mit dem alten Punkt verbunden. Da sich der Grafikcursor zu Beginn im Punkt(0, 0) befindet, muss er mit pos(x, y) auf den ersten Funktionspunkt gesetzt werden.
# Gp12a.py from gpanel import * makeGPanel(-6, 6, -30, 30) drawGrid(-5, 5, -25, 25, "gray") setColor("blue") lineWidth(2) x = -5 while x < 5: y = x ** 3 - 9 * x pos(x, y) if x == -5 else draw(x, y) x = x + 0.01 |
|
Erklärungen zum Programmcode:
| y = x ** 3 - 9 * x Der Potenzoperator wird in Python mit 2 Sternen geschrieben |
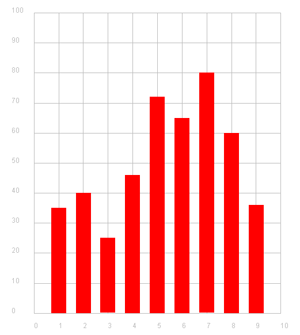
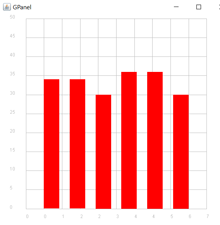
Beispiel 2: Erstellen eines Häufigkeitsdiagramms (Säulendiagramm)
Im Beispiel werden die Werte einer Liste, die zum Beispiel die Ergebnisse einer statistischen Untersuchung darstellen, in einer Balkengrafik dargestellt. Für die Darstellung verwendet man hier die Funktion fillRectangle().
# Gp12b.py from gpanel import * makeGPanel(-1, 11, -10, 110) drawGrid(0, 10, 0, 100, "gray") values = [35, 40, 25, 46, 72, 65, 80, 60, 36] setColor("red") x = 1 for y in values: fillRectangle(x - 0.3 , 0, x + 0.3 , y) x = x + 1 |
 |
Beispiel 3: Verwendung des Python-Moduls math
Python verfügt über viel mathematische Funktionen. Um diese zu verwenden, muss man das Modul math importieren.
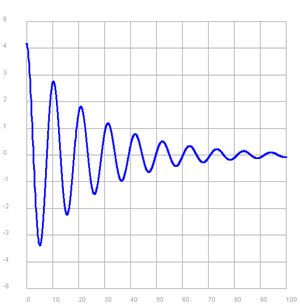
Die aus der Physik bekannte Funktion y = ae-kx sin(ωt + π/2)
stellt eine gedämpfte harmonische Schwingung dar. Die Funktionswerte werden mit Hilfe von Funktionen exp() , sin(), pi aus dem Modul math berechnet. Die Dokumentation zum Modul math findet man im Internet, z. B. unter https://docs.python.org/2/library/math.html. Man kann sie direkt im Menü von TigerJython unter Hilfe/Python Docs anzeigen lassen.
# Gp12c.py from gpanel import * from math import exp, sin, pi makeGPanel(-10, 110, -7, 7) drawGrid(0, 100, -6, 6, "gray") setColor("blue") lineWidth(3) x = 0 a = 5 k = 0.04 omega = 0.6 while x < 100: y = a * exp(-k * x) * sin(omega * x + pi/2) pos(x, y) if x == 0 else draw(x, y) x = x + 0.1 delay(8) |
 |
| Aufgaben: Serie 12 |
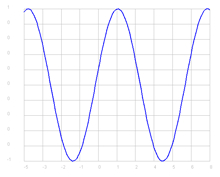
1) |
y = math.sin(x) aufrufen, da die mathematische Funktionen im Modul math sind. |
 |
2) |
Mit dem untenstehenden Programm wird das Würflen simuliiert. Ein Würfel wird 200 mal geworfen und die Anzahl Ereignisse mit 1, 2, 3, ..., 6 in der Liste a gespeichert. from gpanel import * from random import randint a = [0, 0, 0, 0, 0, 0] n = 200 for i in range(n): r = randint(1, 6) if r == 1: a[0] += 1 elif r == 2: a[1] += 1 elif r == 3: a[2] += 1 elif r == 4: a[3] += 1 elif r == 5: a[4] += 1 elif r == 6: a[5] += 1 print(a) Stelle die Höufigkeiten mit einem Säulendiagramm dar. |
 |
3) |
|
 |