13. Simulationen
Die Koordinatengrafik eignet sich hervorragend für die Visualisierung von Simulationen. Zusätzlich können die simulierten Daten mit Python einfach rechnerisch ausgewertet werden.
Beispiel 1: Würfelsimulation
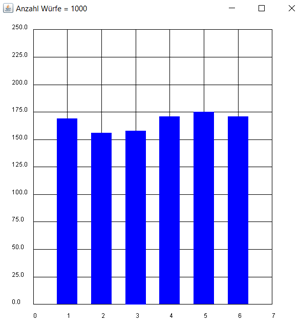
Mit Hilfe von Zufallszahlen wird das Werfen eines Würfels simuliert. Die Funktion randint(1, 6) aus dem Modul random liefert zufällige Würfelzahlen (1, 2, ...6). In Ihrem Programm werden 1000 solche Würfelzahlen erzeugt und die Häufigkeiten, mit welchen die einzelnen Zahlen vorkommen, in einer Liste p erfasst und mit einem Häufigkeitsdiagramm dargestellt.
Experimenteren Sie mit verschiedenen n. Je grösser n, umso gleichmässiger sollte die Häufigkeits-Verteilung ausfallen.
from gpanel import *
from random import randint
n = 1000
p = [0] * 7
repeat n:
a = randint(1, 6)
if a == 1:
p[1] += 1
elif a == 2:
p[2] += 1
elif a == 3:
p[3] += 1
elif a == 4:
p[4] += 1
elif a == 5:
p[5] += 1
elif a == 6:
p[6] += 1
print(p)
makeGPanel(-1, 8, -2*n/100, n/4 + n/100)
drawGrid(0, 7, 0, n/4, 7, 10)
title("Anzahl Würfe = " + str(n))
setColor("blue")
for i in range(1, 7):
fillRectangle(i-0.3 , 0, i + 0.3, p[i])
|
|
|
Erklärungen zum Programmcode:
 |
p = [0] * 7: Erstellt eine Liste mit 7 Nullen. (Die erste Null nur wegen der grafischen Darstellung) |
 |
drawGrid(0, 7, 0, n/4, 7, 10): Die ersten 4 Parameter legen die Koordinaten der x- und y-Achse fest, mit den letzten zwei kann man die Anzahl Ticks auf der x- und y-Achse festlegen |
Beispiel 2: Mittlere Wartezeit beim Würfelspiel
Man wirft einen Würfel. Wir stellen uns die Frage, wie oft muss man im Mittel würfeln, bis eine bestimmte Zahl, z.B. eine 6 vorkommt. Stellt man sich vor, dass jeder Wurf gleich viel Zeit benötigt, so handelt es sich um die Frage nach der mittleren Wartezeit.
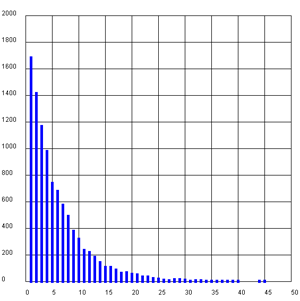
Statt mathematisch vorzugehen, simuliert man das Würfeln mit Zufallszahlen 1, 2, 3, ...6 und wiederholt dieses Experiment, bis die Zahl 6 vorkommt. Die Zahl der benötigen Versuche wird in der Variablen k gespeichert. Man wiederholt das Experiment 10000 mal und stellt die Häufigkeiten in einem Häufigkeitsdiagramm dar. Gleichzeitig bildet man die Summe von k, damit man am Schluss die mittlere Wartezeit berechnen kann. Diese wird im Titel angezeigt. Um Die Simulation zu verstehen, experimentieren Sie zuerst mit kleinen n-Werten (z. Bsp. n = 5, n = 10, n = 100).
# Gp13a.py
from gpanel import *
from random import randint
n = 10000
def sim():
k = 1
r = randint(1, 6)
while r != 6:
r = randint(1, 6)
k += 1
return k
makeGPanel(-5, 55, -200, 2200)
drawGrid(0, 50, 0, 2000)
title("Waiting on a 6")
setColor("blue")
h = [0] * 51
lineWidth(5)
count = 0
repeat n:
k = sim()
print(k)
count += k
if k <= 50:
h[k] += 1
line(k, 0, k, h[k])
mean = count / n
title("Mean waiting time = " + str(mean))
|
|

|
Erklärungen zum Programmcode:
 |
sim(): Gibt die Anzahl Würfe zurück, bis die Zahl 6 vorkommt |
 |
h = [0] * 51: Erstellt eine Liste mit 51 Nullen |
Beispiel 3: Berechnung des Zahl PI mit der Monte-Carlo-Methode
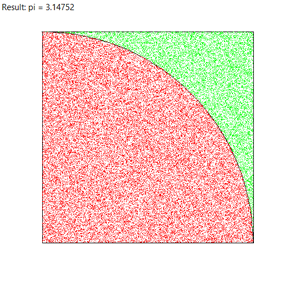
Es handelt sich um ein klassisches Beispiel einer Computersimulation. Auf ein Quadrat mit der Seitenlänge 1 wird eine grosse Zahl n Zufallspunkte geworfen. Der Anteil der Punkte innerhalb des Viertelkreises entspricht offensichtlich ungefähr seinem Flächenanteil.
Wirft man also n Punkte und befinden sich die Zahl hits innerhalb des Viertelkreises, so gilt
hits / n = Viertelkreisfläche / Quadratfläche
Mit einem GPanel lässt sich die Aufgabe grafisch und rechnerisch lösen.
# Gp13b.py
from gpanel import *
from random import random
makeGPanel(-0.3, 1.3, -0.3, 1.3)
rectangle(0, 0, 1, 1)
arc(1, 0, 90)
hits = 0
n = input("Number of rain drops")
i = 0
while i < n:
x = random()
y = random()
if x*x + y*y < 1:
hits = hits + 1
setColor("red")
else:
setColor("green")
i = i + 1
point(x, y)
pi = 4 * hits / n
title("Result: pi = " + str(pi))
|
|
 |
Erklärungen zum Programmcode:
 |
n = input(): Die gewünschte Anzahl Zufallspunkte kann in einem Inputdialog eingegeben werden |
 |
pi = 4 * hits/n: Die Fläche des Viertelreises mit dem Radius 1 ist pi/4, die Fläche des Quadrats ist 1. Also ist hits/n = pi/4 oder pi = 4 * hits / n |
Beispiel 4: Simulation eines senkrechten Wurfs
Mit der Beschleunigung a ist in einem kleinen Zeitintervall dt die neue Geschwindigkeit vneu = v + a * dt und der neue Ort xneu = x + v * dt. Hier ist die Beschleunigung a = -g. Der neue Zustand wird alle 0.05 Sekunden berechnet.
# Gp13c.py
from gpanel import *
import time
makeGPanel(-6, 6, -220, 70)
setColor("red")
enableRepaint(False)
g = 9.81
dt= 0.05
t = 0; y = 0
v = 25
while t < 10:
v = v - g * dt
y = y + v * dt
t = t + dt
drawGrid(-5, 5, -200, 50, "gray")
pos(0, y)
fillCircle(0.3)
repaint()
time.sleep(dt)
clear()
|
|
 |
Erklärungen zum Programmcode:
 |
enableRepaint(False): Es handelt sich um einen Animation. Um das Flackern zu vermeiden, wird das automatische Rendering abgeschaltet |
1)
|
Bei einem Spiel werden 3 Würfel gleichzeitig geworfen. Der Spieler A gewinnt, wenn mindestens ein Sechser geworfen wird. Der Spieler B gewinnt, wenn kein Sechser vorkommt. Wer hat die bessere Gewinnchance, wenn das Spiel beliebig oft wiederholt wird?
|
|
|
2) |
Man stellt sich die Frage, wie oft man im Mittel würfeln muss, um alle Würfelzahlen 1, 2, 3, 4, 5, 6 mindestens einmal zu erhalten.
Löse die Frage mit einer Simulation.
|
|
|
3)
|
Simuliere das Werfen zweier Münzen und stelle die Häufigkeiten, mit welchen die Ereignisse "zweimal Zahl", "einmal zahl und einmal Kopf", und "zweimal Kopf" eintreten, mit einem Häufigkeitsdiagramm dar.
|
|
|
4)
|
Im Beispiel 4 wird ein senkrechter Wurt simuliert. Analog kann man auch den Schiefen Wurf simulieren. Ein Körper wird unter dem Winkel von 45° mit der Anfangsgeschwindigkeit 32 geworfen. Stelle seine Laufbahn während 10 Sekunden grafisch dar. Um die Funktionen sin und cos zu verwenden, musst du folgende Importzeile hinzufügen:
from math import sin, cos, pi
Als Vorlage kannst du das Beispiel 4 verwenden und die physikalischen Formel mit denjenigen für den schiefen Wurf ersetzen:
g = 9.81
dt = 0.05
v = 32
alpha = pi/4
t = 0; x = 0; y = 0
vx = v * math.cos(alpha)
vy = v * math.sin(alpha)
while t < 10:
vy = vy - g * dt
x = x + vx * dt
y = y + vy * dt
Bemerkung: Der Winkel in den Funktionen sin() und cos() muss in Radian angegeben werden. pi/4 entspricht dem Winkel 45°. Für die Umrechnung kann die Funktion radians(alpha), die Winkel in Grad in Winkel in Radian umrechnet, verwendet werden. Diese muss zusätzlich importiert werden.
|
|
|



