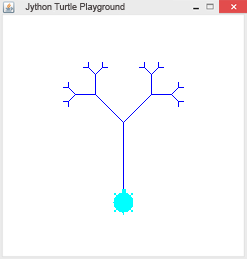
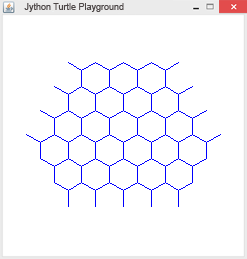
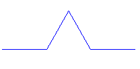
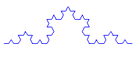
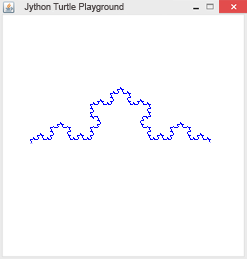
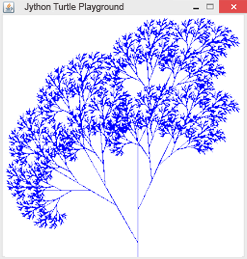
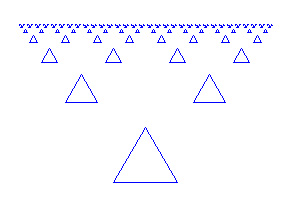
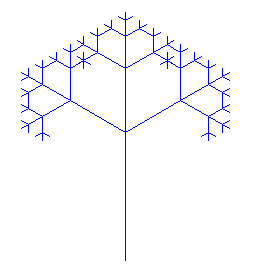
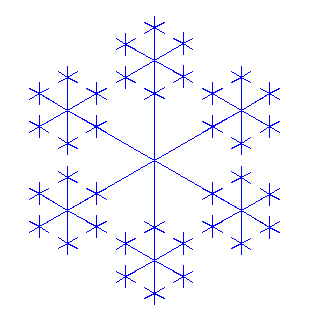
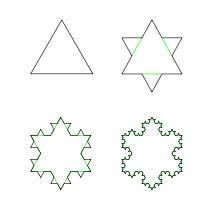
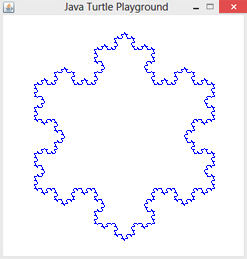
Rekursion ist ein Lösungsverfahren, bei dem ein Problem auf das gleichartige, aber etwas vereinfachte Problem zurückgeführt wird. Eine Funktion ist dann rekursiv, wenn sie sich selbst aufruft. Damit sich eine rekursive Funktion nicht endlos aufruft, braucht sie eine Abbruchbedingung ("Verankerung"). Die Turtlegrafik eignet sich hervorragend für die Programmierung von Rekursionen. Es entstehen dabei sehr schöne Bilder.

Beispiel 1: Das Prinzip einer Rekursion kann anschaulich am Beispiel Zeichnen einer Treppe erklärt werden: Bei der rekursiven Lösung wird eine Treppe mit 6 Stufen aus einer Stufe und einer Treppe mit 5 Stufen zusammengesetzt, ein Treppe mit 5 Stufen kann auf eine Stufe und einer Treppe mit 4 Stufen zurückgeführt werden (usw). In der Funktion staircase(n) wird jeweils dieselbe Funktion staircase(n - 1) aufgerufen, wobei der Parameter bei jedem neuen Aufruf um 1 kleiner wird. Wenn die Abbruchbedingung n = 0 erfüllt ist, bricht das Programm ab.

Beispiel 2: Der binäre Baum

Das Zeichnen eines binären Baums lässt sich auf eine einfache Grundfigur zurückführen. Die Funktion tree() wird jeweils im linken und rechten Ast mit der halben Streckenänge s aufgerufen. Für s < 8 bricht die Rekursion ab.

# Tree.py

from gturtle import *

def tree(s):
    if s < 8:
        return
    forward(s)
    left(45)
    tree(s/2)
    right(90)
    tree(s/2)
    left(45)
    back(s)

makeTurtle()
setY(-100)
tree(128)

Beispiel 3: Wabenmuster
Wenn man die Länge der gezeichneten Linien immer gleich behält und den Drehwinkel 60° wählt erhält man einen schönen Wabenmuster.

# Wabenmuster.py

from gturtle import *

def wabe(s):
    if s == 0:
        return
    forward(a)
    left(60)
    wabe(s - 1)
    right(120)
    wabe(s - 1)
    left(60)
    back(a)

makeTurtle()
hideTurtle()
a = 20
s = 12
wabe(s)

Beispiel 4: Quadratmuster
Das erste Quadrat hat die Seitenlänge 64. Bei jedem weiteren Aufruf der Funktion figure() wird die Seitenlänge halbiert. Die Rekursion bricht ab, wenn s < 1 ist. Ergänzt man die Funktion figure() mit folgenden zwei Zeilen
figure(x - s, y - s, s/2)
figure(x + s, y - s, s/2)
so werden Quadrate auch im unteren Bereich gezeichnet. Mit gefüllten Quadraten entsteht ein schönes Teppichmuster.

 # SquarePattern.py

from gturtle import *

def square(s):
    for i in range(4):
        forward(s)
        right(90)

def figure(x, y, s):
    if s < 2:
        return
    setPos(x - s/2, y - s/2)
    square(s)
    figure(x + s, y + s, s/2)
    figure(x - s, y + s, s/2) 

makeTurtle()
speed(-1)
figure(0, 0, 64)

Beispiel 5: Koch-Kurve
Zum besseren Verständnis kann man die Anzahl Generationen auf 1, 2, oder 3 reduzieren:

1 Generation	2 Generationen	3 Generationen

# Koch.py from gturtle import * def koch(s, n): if n == 0: forward(s) return koch(s / 3, n - 1) left(45) koch(s / 3, n - 1) right(90) koch(s / 3, n - 1) left(45) koch(s / 3, n - 1) makeTurtle() hideTurtle() setPos( -180, 0) right(90) koch(200, 4)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Beispiel 6: Peano

Peano ist eine der bekanntesten Rekursion. Das Problem lässt sich auf eine einfache Figur zurückführen.

 # Peano.py

from gturtle import *

def peano(n, s, w):
    if n == 0:   
        return
    lt(w)
    peano(n - 1, s, -w)
    fd(s)
    rt(w)
    peano(n - 1, s, w)
    fd(s)
    peano(n - 1, s, w)
    rt(w)
    fd(s)
    peano(n - 1, s, -w)
    lt(w)
    
makeTurtle()
setPos(185, -185)
speed(-1)
peano(6, 6, 90)

Beispiel 7: TreeFractal

# TreeFractal.py

from gturtle import *

def tree(size):
    if size < 5:
        fd(size)
        bk(size)
        return
      
    fd(size / 3)
    lt(30)
    tree(size * 2 / 3)
    rt(30)
    fd(size / 6)
    rt(25)
    tree(size / 2)
    lt(25)
    fd(size / 3)
    rt(25)
    tree(size / 2)
    lt(25)
    fd(size / 6)
    bk(size)

makeTurtle()
ht()
setPos(20, -195)
tree(250)

Beispiel 8: FlowerFractal

# Tu10a.py

from gturtle import *

def figur(size, angle, turn):
    if size < 10:
        return
    while True:  
        flower(size, angle)
        turn = turn + angle
        if turn % 360 == 0:
            break       
def flower(size, angle):
    forward(size)
    dot(15)
    figur(size/2, -angle, 0)
    right(angle)    

makeTurtle()
setPos(-80, -80)
figur(64, 60, 0)

Beispiel 9: Sierpinsi Fraktal

# Sierpi.py

from gturtle import *

def triangle(s):
   repeat 3:
      forward(s)
      left(120)   

def sierpi(n, s):
   if n == 0: 
      triangle(s)  
      return
   sierpi(n - 1, s / 2)
   forward(s / 2)
   sierpi(n - 1, s / 2)
   left(120)
   forward(s / 2)
   right(120)
   sierpi(n - 1, s / 2)
   left(60)
   back(s / 2)
   right(60)
    
makeTurtle()
n = 7
s = 400
hideTurtle()
setPos( -200, -190)
right(90)
sierpi(n, s)

Ergänze den Programmcode so, dass eine Flocke gezeichnet wird.

def figure(s):
    
    for i in range(6):
        forward(s)
        figure(s/3)
        back(s)
        right(60)

Ergänze die Kochkurve so, dass eine ganze Schneeflocke entsteht.

Anleitung: Betrachte folgende Generationen::

Die interessante Klothoide kann mit folgender rekursiven Funktion erstellt werden:

def clothoid(s):     
    if s > 1500:
        return
    forward(20)
    left(0.025 * s)
    clothoid(s + 10)

Ergänze den Programmcode und teste die Rekursion für verschiedene Parameter s.