Turtle und Sound


Die Turtle kann verschiedene Töne abspielen. Dazu wird die Funktion playTone(frequency, duration) verwendet. Der erste Parameter bestimmt die Tonfrequenz in Hz, der zweite Parameter die Abspieldauer in Millisekunden. Hier einige Tonfrequenzen :
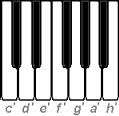
Ton Frequenz Ton Frequenz    
h' 495 h'' 988    
a' 440 a'' 880    
g' 396 g'' 784    
f' 352 f'' 698    
e' 330 e'' 660    
d' 297 d'' 588    
c' 264 c'' 524 c''' 1048

Diese Frequenzen lassen sich berechnen. Wenn man von einem Grundton (z. Bsp. a' mit f = 440 Hz) ausgeht, erhält man die Frequenz des darauf folgenden Halbtons mit dem Faktor 1.05946 und den nächsten ganzen Ton mit dem Faktor 1.05946 * 1.05946 ≈ 1,122. (z. Bsp. h' = 440 * 1.122 = 494). Die Frequenzen in der Tabelle sind gerundet.

Warum diese Faktoren? Eine Oktave (Frequenzverhältnis c'' : c' = 2 : 1) ist in zwölf Halbton-Schritte aufgeteilt.
Ein Halbton = 1/12·Oktave, dies entspricht dem Frequenzverhältnis .

 

Beispiel 1: Eine Melodie spielen
Hier sollen mehrere Töne nacheinander abgespielt werden. Die zugehörigen Tonfrequenzen werden in einer Liste zusammengefasst. Mit einer for-Schleife kann man dann die Liste durchgehen und die Töne mit der Funktion playTone() abspielen. 

# Tu14.py

from gturtle import *
      
song = [262, 294, 330, 349, 392, 392, 392, 0, 440, 440, 440, 440, 392]

for f in song:
    playTone(f, 200)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)
 

Erklärungen zum Programmcode:

for f in song : geht alle Elemente f der Liste song durch
playTone(f, 200) : spielt Tone mit der Frequenz f 200 Millisekunden lang

 

Beispiel 2: Die Turtle zeichnet eine Treppe und spielt dabei immer höhere Töne. Wenn man eine c-dur Tonleiter abspielen will, muss man die Halbtöne zwischen e' und f' und zwischen h' und c'' beachten. Nach 3 ganzen Tönen folgt ein Halbton, dann wieder 3 ganze Töne und ein Halbton.

# Tu14a.py

from gturtle import *

def step():    
    forward(30) 
    right(90)
    forward(30) 
    left(90)   
      
makeTurtle()
hideTurtle()
f = 262
r = 1.059463

for i in range(2):
    for k in range(3):
        step()
        f = f * r * r
        playTone(f, 200)
    step()
    f = f * r
    playTone(f, 200)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)
 

Erklärungen zum Programmcode:

f = f * r * r : Frequenz des nächsten ganzen Tons
f = f * r : Frequenz des nächsten Halbtons

 

Beispiel 3: Nicht blockierende Funktion playTone().
Im Beispiel 2 wurde beim Zeichnen der Treppenstufen die Turtle versteckt, damit das Zeichnen schneller erfolgt. Wenn man aber die Turtle beim Zeichnen sichtbar macht, ist es störend, dass die Funktion playTone() blockierend ist. Das Programm wartet bei jeder Treppenstufe bis der Ton fertig abgespielt ist und beginnt erst anschliessend die nächste Treppenstufe zu zeichnen. Wenn man will, dass das Abspielen des Tons und das Zeichnen gleichzeitig erfolgt, muss man eine nicht blockierende Funktion playTone() verwenden. Den Unterschied sieht man deutlich, wenn man im folgenden Beispiel statt der nicht blockierende die blockierende Funktion aktiviert.

# Tu14b.py

from gturtle import *

def step():    
    forward(30) 
    right(90)
    forward(30) 
    left(90)   
      
makeTurtle()
f = 262
r = 1.059463

for i in range(2):
    for k in range(3):
        f = f * r * r
        playTone(f, 500, block = False)
        # playTone(f, 500)
        step()        
    f = f * r
    playTone(f, 500, block = False)
    step()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)
 

 

Erklärungen zum Programmcode:

playTone(f, 500, block = False) : nicht blockierende Funktion, die sofort zurückkommt und nicht erst nach 500 Millisekunden

 

Beispiel 4: Ein einfaches Klavier
Mit zwei for-Schleifen werden die weisse und schwarze Tasten einer Oktave gezeichnet.
Per Mausklick kann eine Melodie gespielt werden. Aus der x-Koordinate des Mausklicks kann berechnet werden, welche Taste geklickt wurde. Bei den schwarzen Tasten wird zusätzlich die Funktion getPixelColor() verwenden, die die Farbe der Unterlage zurück gibt.

 

    
  

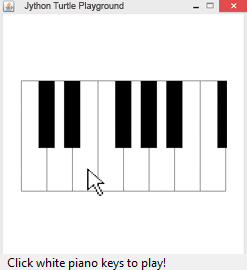# Tu14c.py

from gturtle import *

def drawPiano():
    setPenColor("black")
    for x in range(-200, 160, 50):
        setPos(x, -100)
        for k in range(2):
            fd(216).rt(90).fd(50).rt(90)
    setPenWidth(32)
    for x in [-150, -100, 0, 50, 100, 200]:
        setPos(x, 0)
        fd(100)

def onMouseHit(x, y):
    if x > -200 and x < 215 and y > -100 and y < 100:
        i = int((x + 200)/50)
        setPos(x, y)
        if getPixelColorStr() == "black":
            k = int((x + 215) / 50)
            f = blacktones[k]
        else:
            f = whitetones[i]
        playTone(f, 200)

whitetones = [262, 294, 330, 349, 392, 440, 494, 524]
blacktones = [0, 277, 311, 0, 360, 415, 466, 0, 555]

makeTurtle(mouseHit = onMouseHit)
hideTurtle()
drawPiano()
addStatusBar(20)
setStatusText("Click a piano key to play!")
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Erklärungen zum Programmcode:

drawPiano() : zeichnet eine Klavier-Oktave
onMouseHit(x, y) : wird beim Mausklick aufgerufen, liefert die Koordinaten des Mausklicks
getPixelColorStr() : liefert die Hintergrundfarbe an der aktuellen Turtleposition
i = int((x + 200)/50) : berechnet in welchem Rechteck der Mausklick erfolgt hat
f = tones[i] : holt das i-te Element der Liste tones

 

Beispiel 5: Eine Zufallsmelodie
Zuerst wird eine Klaviertastatur gezeichnet. Die Turtle wählt zufällig eine der 13 gezeichneten Tasten, bewegt sich auf diese Position und spielt den entsprechenden Ton ab. So spiel sie selbständig eine kurze Melodie, die je nach Zufall auch schön tönen kann..

In der Funktion playTon() können anstelle der Frequenzen auch die Ton-Name verwendet werden (z. Bsp. c', d', e' usw.) . Wenn man die Töne in einer Liste zusammenfassen will, muss man die Bezeichner in Anführungszeichen setzten. Vorteil dieser Schreibweise besteht insbesondere darin, dass zusätzlich auch Instrument gewählt werden kann. Erlaubt sind piano, quitar, harp, trumpet, organ und violin.

    
  

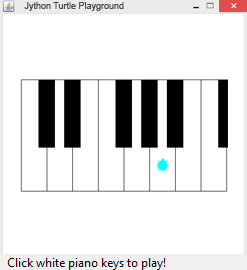# Tu14d.py

from gturtle import *
import random

def drawPiano():
    setPenColor("black")
    for x in range(-200, 160, 50):
        setPos(x, -100)
        for k in range(2):
            fd(216).rt(90).fd(50).rt(90)
    setPenWidth(32)
    for x in [-150, -100, 0, 50, 100, 200]:
        setPos(x, 0)
        fd(100)

whitetones = ["c'", "d'", "e'", "f'", "g'", "a'", "h'", "c''"]
blacktones = ["c#'", "d#'", "f#'", "g#'", "a#'", "c#''"] 

makeTurtle()
hideTurtle()
drawPiano()
showTurtle()

for n in range(30):
    i = random.randint(0, 13)
    if i < 8:
        x = i * 50 - 175
        setPos(x, -50)
        f = whitetones[i]
    else:
        blackPos = [-150, -100, 0, 50, 100]
        k = i - 9 
        x = blackPos[k]
        setPos(x, 30)    
        f = blacktones[k]
    playTone(f, 100, instrument = "piano")
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Erklärungen zum Programmcode:

whitetones = ["c'", "d'", "e'", "f'", "g'", "a'", "h'", "c''"] : Liste der weissen Tasten mit Noten-Namen
blacktones = ["c#'", "d#'", "f#'", "g#'", "a#'", "c#''"] : Liste der schwarzen Tasten
i = random.randint(0, 13) : erzeugt eine ganzzahlige Zufallszahl zwischen 0 und 13
x = i * 50 - 175 : berechnet die x-Koordinate der weissen Tasten
x = blackPos[k] : holt die x-Kaaordinate der schwarzen Taste aus der Liste blackPos

 
Aufgaben Serie 14

1)

Erstelle eine Liste song mit Tonfrequenzen und spiele die Melodie ab.

Mit for f in reversed(song): kannst du die Töne in umgekehrten Reihenfolge abspielen.

2)

Spiele alle 12 Tonfrequenzen einer c'' - c''' Oktave (inklusive Halbtöne) und zeichne dazu immer grössere Quadrate.

Spiele dann die Töne in der umgekehrten Reihenfolge (zuerst den höchsten Ton) und zeichne dazu rote Quadrate (zuerst das grösste Quadrat).

  

3) Ändere das Beispiel 4 so, dass bei den weissen und schwarzen Tasten die Notennamen statt Frequenzen gegeben werden. Dann kannst du in der Funktion playTone() auch das Instrument wählen.