TigerJython xx
 für Gymnasien

14. Fraktale

Fraktale sind computergenerierte Bilder, die eine Selbstähnlichkeit aufweisen, d.h. bei denen Teilbilder eine verkleinerte Kopie des Gesamtbildes sind. Der Begriff fractal wurde 1975 von Mathematiker Benoit Mandelbrot eingeführt und stammt aus dem Lateinischen fractus (gebrochen), was sich auf die sogenannte fraktale Dimension bezieht. In der traditionellen Geometrie ist eine Linie eindimensional, eine Fläche zweidimensional und ein Raum dreidimensional. Fraktale Bilder weisen meist eine nicht-ganzzahlige Dimension auf. Interessante Bilder liefern Fraktale, die durch eine nichtlineare Transformation entstehen. Solche Fraktale werden in der Regel iterativ berechnet und verwenden häufig komplexe Zahlen.

Im Folgenden findet man den vollständigen Programmcode zu einigen bekannten Fraktalen ohne weiteren Kommentar. Auch ohne eingehendes Studium des Programmcodes kann man sich an den schönen Bildern freuen und Frakale mit anderen Farben erstellen.

   


Beispiel 1: Farn

# Farn.py

from gpanel import *
import random

def farn():
    z = 0
    n = 0
    while n < nbPoints:
        r = random.random()
        c = "black"
        if r < 0.01:
            c = "yellow"
            z = f(z, 0, 0, 0, 0.16, 0, 0) # Stiel
        elif r < 0.86:
            c = "green"
            z = f(z, 0.85, 0.04, -0.04, 0.85, 0, 1.60) # symmetry
        elif r > 0.86 and r < 0.93:
            c = "red"
            z = f(z, 0.20, -0.26, 0.23, 0.22, 0, 1.60)  # left leaves
        elif r > 0.93:
            c = "blue"
            z = f(z, -0.15, 0.28, 0.26, 0.24, 0, 1.44) # right leaves
        setColor(c)
        point(z)
        n += 1

def f(z, a, b, c, d, e, f):
    re = a * z.real + b * z.imag + e
    im = c * z.real + d * z.imag + f
    return complex(re, im)

makeGPanel(-3.5, 3.5, 0, 10)
bgColor("black")
title("Creating fert...")
nbPoints = 40000
farn()
title("Creating fern...     done.");
► In Zwischenablage kopieren		  


 

Beispiel 2: Julia

# Julia.py

from gpanel import *

def putPixel(z, c):
  setColor(c)
  point(z.real, z.imag)


maxIter = 100
maxNorm = 50.0
step = 0.005
range = 2.0
makeGPanel(-range, range, -range, range)
c = complex(-0.5, -0.5)
z0 = complex(-range, -range)
enableRepaint(False)
while z0.imag < range: # outer loop in imag direction
    z0 = complex(-range, z0.imag + step)
    while z0.real < range: # inner loop in real direction
        z0 = z0 + step
        z = z0;
        it = 0
        while (z.real * z.real + z.imag * z.imag) < maxNorm and it < maxIter:
            z = z * z + c
            it = it + 1
        if it < 3:
            putPixel(z0, "darkblue")
        elif it < 5:
            putPixel(z0, "green")
        elif it < 8:
            putPixel(z0, "red")
        elif it < 12:
            putPixel(z0, "blue")
        elif it < 100:
             putPixel(z0, "yellow")
        else:
            putPixel(z0, "black")
    repaint()
► In Zwischenablage kopieren		    


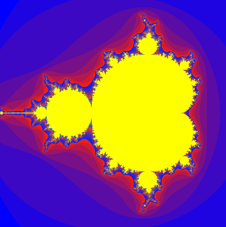
Beispiel 3: Mandelbrot

#Mandelbrot.py

from gpanel import *

def getIterationColor(it):
    color = makeColor((30 * it) % 256, 
                      (4 * it) % 256, 
                      (255 - (30 * it)) % 256)
    return color
    
def mandelbrot(c):
    z = 0
    for it in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return it
    return maxIterations

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.003
ymin = -1.5
ymax = 1.5
ystep = 0.003

makeGPanel(xmin, xmax, ymin, ymax)
title("Mandelbrot set")
enableRepaint(False)
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        itCount = mandelbrot(c)
        if itCount == maxIterations: # inside Mandelbrot set
            setColor("yellow")
        else: # outside Mandelbrot set
           setColor(getIterationColor(itCount))
        point(c)
        x += xstep
    y += ystep
    repaint()
► In Zwischenablage kopieren