TigerJython xx
 für Gymnasien

Serie 7: Funktionen


1)
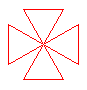
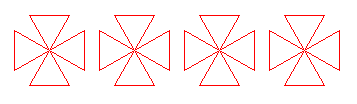
 Erstelle folgende Zeichnung, in dem du zuerst eine Funktion dreieck definierst. Die Funktion kleeblatt() besteht aus vier Dreiecken. Mit Hilfe der Funkion setPos(x, y) kann man Kleeblätter an verschiedenen Positionen zeichnen. Zum Spass kannst du die Figuren noch füllen.
 
       



2) Zeichne eine Europa-Flagge, indem du zuerst eine Funktion star(), die einen Stern zeichnet, definierst. Die blaue Hintergrundfarbe erhälst du mit dem Befehl clear("blue").

 

 

3)

Zeichne Blumen in verschiedenen Farben an verschidenen Positionen.

Verwende dabei die Funktionen
arc()
pental()
flower(x, y, color)

 

 



4)

Verwende Funktionen mit Parametern, um Kleeblätter in verschiedenen Grössen und Farben zu zeichnen.
 

 

 



5)

Definiere eine Funktion zickzack, die eine Zickzack-Linie zeichnet. Diese soll enden, wenn die x- oder y-Koordinate aus dem Bereich (-250, 250) herauskommt. Mit getX() bzw. getY() kannst du die aktuellen Turtle-Koordinaten abfragen. Im Haupprogramm sollen 36 solche zickzack-Linien gezeichnet werden, wobei jede Linie an der Position (0, 0) startet und vor der nächsten Linie eine Drehung um 10° erfolgt.

(Um das Ende der Zickzack-Linie zu bestimmen kannst du z.B. folgende while-Bedingung verwenden:
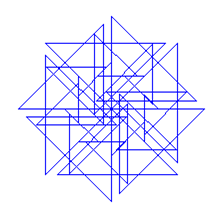
while getX()>-250 and getX()< 250 and getY()>-250 and getY()< 250:

 

 

 



6)

Zum Ausprobieren: SPIROLATERALE
Spirolaterale entstehen durch wiederholtes Zeichnen einer Basisfigur, die durch einen Drehwinkel (a), Anzahl Segmente (q), Länge des ersten Segnmentes (s) und Anzahl Wiederholungen (n) definiert ist.

   
a = 90, q = 7, s = 20, n = 4  
a = 36, q = 12, s = 15, n = 5
   a = 45, q = 7, s = 20, n = 20 

# Tu7d.py
from gturtle import *

def figure(a, q, s):
    for i in range(1, q):
        forward(s * i)
        left(180 - a)    

makeTurtle()
#hideTurtle()
n = 4
repeat n:
   figure(90, 8, 20)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Experimentiere mit verschiedenen Parametern. Spirolaterale mit figure (90, 8, 20)  oder figure(36, 10, 15) sind nicht geschlossen. Wie muss a, q und n gewählt werden, damit das Spirolateral geschlossen ist?